｢約分の本質｣で小学生でも解ける大学入試問題 図で考える｢公約数の探し方｣最強テクニック

173と174で、その間は1しかありません。861の箱が173個積み上がったのが148953で、174個積み上がったのが149814ということになります。そして、173個＋174個＝347個が積み上がったのが298767となるわけですね。

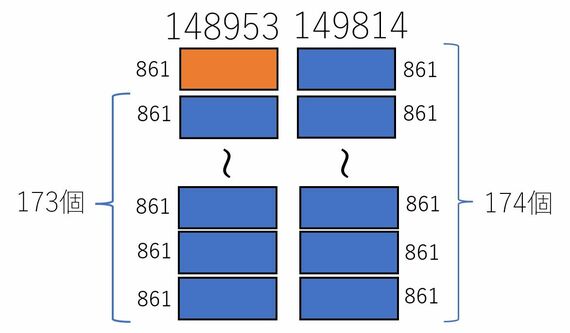
ということで答えは、分母と分子を861で割って、このようになります。

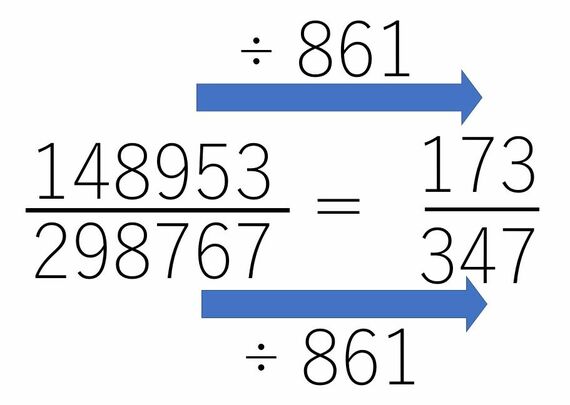
「173/347」が答えになります。一見膨大な計算が必要に見えますが、実はこれだけ圧縮できる問題だったわけです。

「算数の基礎」は数学を学ぶうえでとても大切

いかがでしょうか？ この問題は、「約分とはどういうものか」ということをしっかりと理解し、「差の部分も含めて公約数を探すことができるはず」と考えることができると、解けるようになります。

約分なんて、小学校高学年であれば誰でも習うものです。でも、それがこんなふうに難しくなって、大学入試で出題されることもあるのです。

やはり数学の勉強をするうえで重要なのは、その基礎となる算数の部分です。高校の問題についていけないからといって、高校の勉強を復習していてもなかなかうまくいきません。思い切って、中学校の勉強や小学校の勉強に立ち戻ったほうが、うまく成績が上げられるようになることがあります。

応用問題が解けるようになるためには、基礎問題がしっかり理解できているかどうかが重要だということです。ぜひみなさんも、今回の問題を通して「算数の重要性」を理解してもらえればと思います。