｢約分の本質｣で小学生でも解ける大学入試問題 図で考える｢公約数の探し方｣最強テクニック

これを順番に、「えーとこれ、3で割れるのかな」「7で割ったらどうなるだろう」と計算していくのはとても難しいと思いますし、時間もかかってしまいます。

高校に上がると「ユークリッドの互除法」というものがあるのでそれを使ってもいいのですが、実はこの問題、そんな難しい公式を使わなくても、小学生でも解けます。

「約分」を図でイメージできていますか？

まず、約分とはどのようなものか、みなさんはわかりますか？ 

たとえば6/10は、約分すると3/5です。分母と分子の両方を2で割ることができるから、「6÷2＝3」「10÷2＝5」とすることができるわけです。この両方を割ることのできる「2」という数字を公約数と呼び、基本的にはこの公約数を見つけるのが約分では重要になってきます。

これを図式化すると、このようになります。

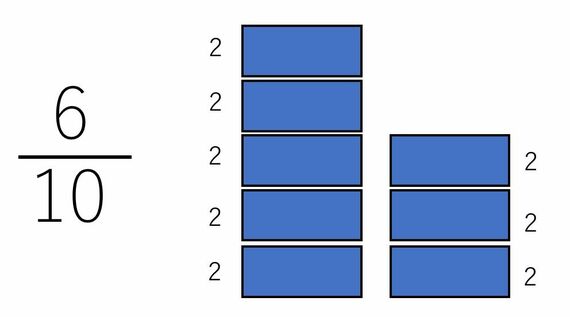
10は「2の箱が5つ重なっている状態」だと表現できて、6は「2の箱が3つ重なっている状態」と表現できるから、3/5になります。9/15は3/5になりますが、これは、15を3の箱が5つ重なっている状態、9を3の箱が3つ重なっている状態と表現できるからですね。

そして、問題なのはこの分母と分子の「差」です。実はこの差も、同じように割り切れるはずなのです。「10＝2の箱が5つ重なっている状態」「6＝2の箱が3つ重なっている状態」なら、「10－6＝4も、2の箱が2つ（5つ－3つ）重なっている状態」だと言えます。

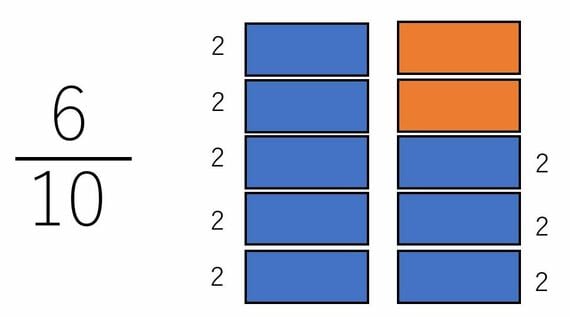
9/15も同じことが言えます。「15－9＝6」で、15も9も6も、全部3で割れますよね。