この「合接の誤謬」が露見する例は、リンダ問題に限りません。とある専門家に対して、「10年後の未来」について予想してもらう問題を出した研究がありました。
あるグループには、「1983年に、アメリカとソ連の外交関係が凍結する」確率を求めさせ、もう1つのグループには、「1983年に、ソ連がポーランドへ侵攻し、アメリカとソ連の外交関係が凍結する」確率を求めさせました。すると、後者のほうが3倍ほど大きな確率を出力したのです。
もちろんこれも上のリンダ問題と同じように、後者のほうが厳しい条件であるため、後者が起こる確率は前者よりも小さくなります。
しかし、当時の国々の状況から、専門家も「ポーランド侵攻によって外交関係の大きな変化が起こるであろう」という代表性ヒューリスティックが無意識のうちにはたらいていたのでしょう。
この「合接の誤謬」は、誰しも持っているものなのです。
このような数値化されたデータを正しく読み取れない、比較できないことは、情報の正誤判定ができないということにつながります。
では、どうすればいいのか。実は高校1年生で習う数学を使って整理することができます。
「数学Ⅰ・A」で登場する「ベン図」で考える
「数学Ⅰ・A」の範囲の中で、「ベン図」というものが出てきます。これは、全体の集合の中で、何か特定の条件を満たす集合を丸い円を描いて表す表現方法のことです。
例えば、1から10までの数字を全体とした場合、「2の倍数」の集合をAとすると、Aに属する数字は2、4、6、8、10の5つになります。これを、
A=｛2,4,6,8,10｝
と表します。そして、Aには5つの数字が属している、という事実を
N（A）=5
と表します。ここでさらに、「3の倍数」の集合Bを考えてみましょう。Bに属する数字は3、6、9の3つであるため、
B=｛3,6,9｝
N（B）=3
と表すことができます。ここで、集合Aにも集合Bにも属している「6」という数字があるため、この2つの集合を表す円は一部が重なり、以下のような図になります。
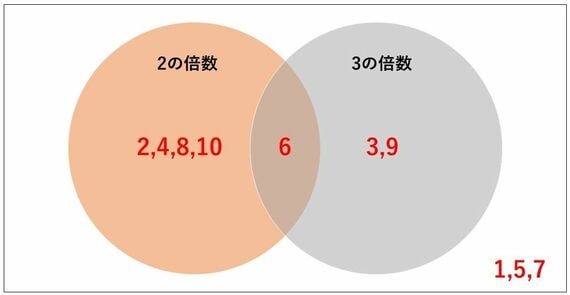
この重なっている部分を、「AかつB」と表すのです。
