確率がわかる人と実はわかっていない人の決定差 人間の非合理さを露呈させる簡単な確率の問題

著名な数学者ポール・エルデシュ（1913─1996）でさえ、当初は反論する側だった。彼は実に多くの論文を書き、共著者も多かったので、エルデシュとの関係の近さを示す「エルデシュ数」〔数が小さいほどエルデシュに近い。エルデシュと直接の共著論文がある人は1、1の人と共著論文があれば2、2の人と共著論文があれば3……と関係が遠ざかるほど数が増えていく〕というのが学者たちの自慢の種になっているほどなのだが、そのエルデシュもマリリンの説に納得がいかなかった。

しかしながら、間違っていたのは反論した学者たちのほうで、“世界一賢い女性”は正しかった。あなたが参加者なら、選択を変えたほうがいい。

選択を「変える」「変えない」でどうなる？

その理由もそれほどややこしくはない。車がどこに置かれているかには、ドア1、ドア2、ドア3の3通りの可能性がある。この3通りそれぞれを考えて、選択を変えない場合と変えた場合の“当たり”の回数を数えてみよう。あなたはドア1を選んだ。これは単なるレッテルなので何番のドアでもいい。モンティが「選ばれていないドアのうちヤギがいるドアを開ける。両方にヤギがいるならその片方をランダムに選ぶ」というルールを守っているかぎり、最初にどのドアを選んでも確率は変わらない。

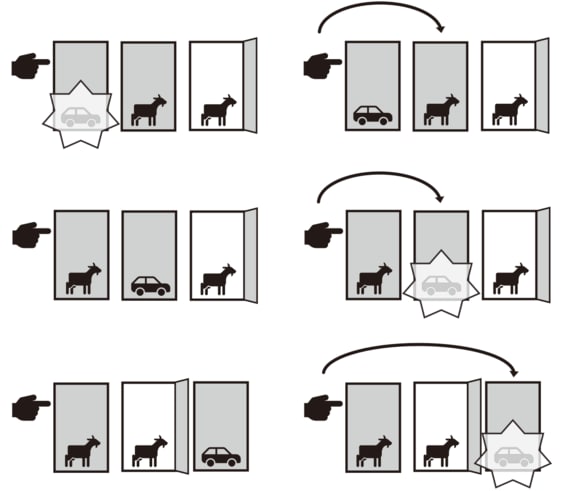
（外部配信先では問題の図版などの画像を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください）

まずあなたが「選択を変えない」場合を考えてみよう（図の左側の列）。図のドアを左から1、2、3とする。車がドア1にあれば、あなたの勝ち（あなたは選択を変えないのだから、モンティがドア2と3のどちらを開けるかは関係ない）。車がドア2にあれば、あなたの負け。車がドア3にあれば、あなたの負け。つまり「選択を変えない」場合の勝率は3分の1である。

次にあなたが「選択を変える」場合を考えよう（図の右側の列）。車がドア1にあれば、あなたの負け。車がドア2にあれば、モンティがドア3を開けるはずなので、あなたはドア2に切り替え、あなたの勝ち。車がドア3にあれば、モンティがドア2を開けるはずなので、あなたはドア3に切り替え、あなたの勝ち。つまり「選択を変える」場合のあなたの勝率は3分の2で、「選択を変えない」場合の2倍になる。

難解というほどのものではない。論理的な可能性など考えずに、切り絵やおもちゃを使って何度かやってみて、勝ち負けを数えてみるだけでわかる。実際モンティ・ホールはそうやってある懐疑的なジャーナリストを説得した（今ならインターネット上でシミュレーションすることもできる）。