計算が速い人が｢公約数･公倍数｣に敏感な深い訳 ｢数の根本的な扱い方｣をマスターしているか

このように、2つの数を分解し、共通点を見つけ、その共通点以外の数をかけ合わせることで、最小公倍数を求められるわけです。この過程というのは、実はいろんな計算で応用できます。

たとえば、分数の足し算の際には、通分を行いますよね。「1/24+1/64」を計算しようとすると、まず24と64を同じ数に直さなければならないわけですが、そのときに「あれ？ これって公倍数どんな感じなんだ？」と悩んでしまうと、計算が遅いですよね。24と64の最小公倍数をすぐに見つけられるようにならないといけないわけです。

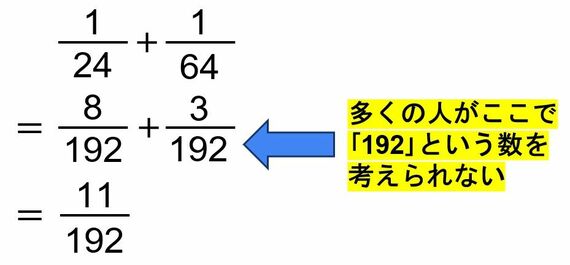
また、計算した後の結果で「11/192」と出てきたとして、これに対して「これって約分できたりするのかな？」と悩んでしまうと、やはりここでも計算が遅くなってしまいます。

11と192の最大公約数は1なのでここは約分できないわけですが、最大公約数を考えられなければ、ここでかなり時間を食ってしまいます。このように、分数が絡んだ問題では、常に最大公約数を意識する必要があるのです。

ですから僕たちも、分数の計算でつまずいている生徒には、分数の勉強の前に「2つの数の最小公倍数を求める訓練」をしてもらいます。これがパッと答えられるようになると、分数の計算なんて楽勝になります。

「算数・数学が苦手」な人にこそ、おすすめ

分数の計算以外にも、ちょっとしたかけ算や割り算でも、大きな数同士の計算でも、最小公倍数がわかっていると解ける問題や、最大公約数がわかっていると計算ミスに気づけるタイミングは多く存在します。

逆に言えば、どんなに難しい問題でも、最小公倍数と最大公約数の勉強をしっかりしていれば計算が速くなり、ミスが少なくなるというわけです。

数学が苦手で困っている場合は、参考にしてみてはいかがでしょうか。