東大生が紹介｢頭の良さ｣を測る奇妙な計算ゲーム なぜ｢数学ができる人は頭が良い｣と言われるか

そして、この式は651でくくることができるので、「651×（1000＋1）」となり、つまりは「651×1001」となります。こういうことですね。

これを見てもらえればわかるとおり、②のプロセスは、ランダムな3桁を「1001倍」しているということにほかならないのです。

1001という数に注目すると…

さて、1001という数に注目しましょう。この数は、素数でしょうか？ そうではないでしょうか？

実はこの数、7で割ることができます。7で割ると「1001÷7＝143」となります。つまり、1001というのは7を約数に持つ、7で割り切れる数なのです。

ここまでを総合して考えてみましょう。「651651」は、「651×1001」でした。つまり651651は、1001を約数に持つのです。そして1001は7で割り切れるので、651651も7を約数に持つということになります。

要するに、「②その数を2つ並べてください」が、元の数を1001倍する操作で、1001は7で割り切れるため、この操作をした数は必ず7で割り切れるというわけなのです。

これはどんな数でも同じことで、他の数で試してもこうなります。

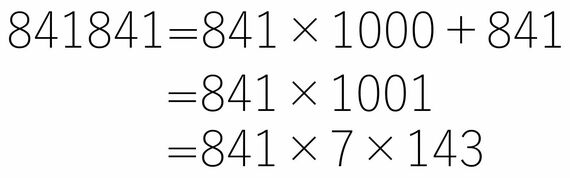
ちなみに同様の理由で、この6桁の数は143でも割り切れる、143の倍数になります。