偶数と奇数｢使いこなせる人｣なら解ける算数問題 知ってはいても｢使いこなせない｣算数の基礎

正解は、1人です。1人以外はあり得ません。

13本は奇数ですから、「偶数＋奇数」の合計になっているはずです。そのうえで、「5＋5＝10」で、パーが2人いても偶数になってしまいます。3人パーの可能性を考えても、「5＋5＋5＝15」なので、本数が13本より多くなってしまいます。

ということは、パーが1人であるとしか考えられないのです。

そして、「13－5＝8」なので、残りは8本で、グーとチョキによってこの8本は構成されています。当然、グーは0本なので、チョキが4人で8本になっていると考えられます。

7人でジャンケンをしているので、「7人－4人（チョキ）－1人（パー）=2人（グー）」となります。ということは、「パーが1人、チョキが4人、グーが2人」となり、これ以外の組み合わせは存在しないとわかります。

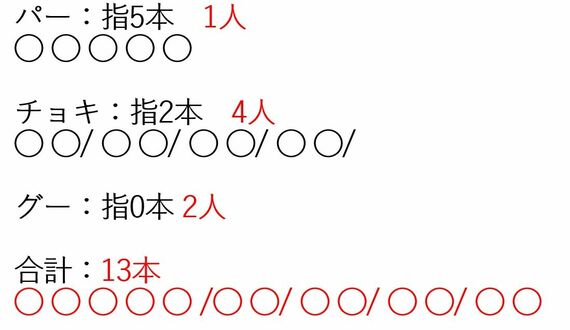
一見すると7人の手をいちいち考えなければならないとても難しい問題のように見えたと思いますが、偶数と奇数の性質を使えば、パーが1人であるということはすぐにわかり、簡単に計算することができましたね。

「偶数と奇数」にはさまざまな応用法がある

このように、偶数と奇数の性質をよく理解することで、数に強くなって、いろんな問題を解くことができるようになったり、計算ミスをしなくなったりします。

たとえば、「375＋6731＋1027＝8132」という計算式を見たときに、0.5秒で、「あ、これ間違っているな」と思える人はどれくらいいらっしゃるでしょう。

数が大きいので気づきにくいですが、これは「奇数＋奇数＋奇数」なので、答えも奇数になるはずなのに、8132は偶数ですよね。それだけで「あれ？ おかしいな？」と考えることができます。

375も6731も1027も8132も、すべて同じ「数」です。ですが、これを2つに分類することで、間違いに気づきやすくなるわけです。

数に強い人というのは、このような分類をきちんと意識することができる人のことなのかもしれません。ぜひ、覚えておいてください。

著者フォローすると、西岡 壱誠さんの最新記事をメールでお知らせします。