東大生なら｢30秒で答えられる｣難解計算クイズ 数式を｢図形に変換する｣といっきに簡単になる

この問題は、ストレートに解こうとすると時間内には解き終わることがなかなか難しい問題だと思います。どんなに44×44の計算が速くても、11×11を一瞬で計算できる人だとしても、30秒以内には計算できない場合が多いと思います。

実はこの問題、掛け算や引き算が速い人よりも、「あること」に気付けた人のほうが速く計算できるのです。

「同じ数のかけ算」から「正方形の面積」を発想する

まず、この計算式には「44」「11」「22」「33」というように、同じ数が並んだ2桁の数字が登場していますね。これらの数は、「44=11×4」「22=11×2」「33=11×3」というように、11の倍数です。

そしてそれらを、「11×11」「22×22」というように、同じ数同士で掛け算をしています。さて、この「同じ数の掛け算」を見て、何か思い出しませんか？ 「11×11」「22×22」というような同じ数の掛け算というのは、「正方形の面積」と同じです。

下の図をご覧ください。

仮に、1辺が11cmの正方形があったとしたら、この正方形の面積は「11cm×11cm」で求められます。今回の「22×22」「33×33」というような数は全部、正方形の面積を求める計算と同じなのです。ですから、これらの計算式は次の図のように置き換えることができます。

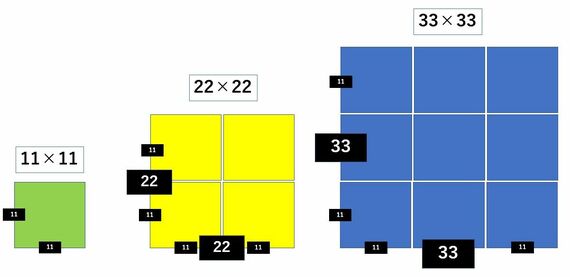
11×11と22×22を比べると、22×22は11×11の正方形を4枚並べた形になるので、4倍大きくなります。同じように考えると33×33というのは11×11の正方形を9枚並べるのと同じになるので、9倍大きいと考えられます。