｢財務力が強い上場企業ランキング｣トップ300 財務面から企業を評価､東京エレクトロンが1位

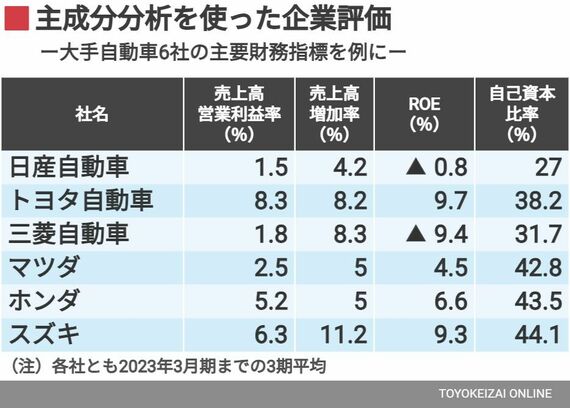
主成分分析は多数のデータをまとめる手法

最後に主成分分析での評価のやり方を主要自動車6社の2023年3月期までのデータを例として簡単にご紹介しておくので参考にしていただきたい。

■線形結合（1次式）とその制約条件

Z＝a×売上高営業利益率＋b×売上高増減率＋c×ROE＋d×自己資本比率

制約条件：a^2＋b^2＋c^2＋d^2 ＝1
Z：主成分（変数の数だけできる。この例だと4つできる。Z ^1・・・Z^4）
a、b、c、d：係数

主成分分析は、こうした多数の変数からなるデータを、情報量を減らさずに新しい変数（主成分）に集約することを目的とする。具体的には、元の変数の線形結合（1次式）を分散（バラツキ）が最大になるように作成する（＝係数の値を決める）。係数と指標の関係が適切であれば、評価値としても使える。

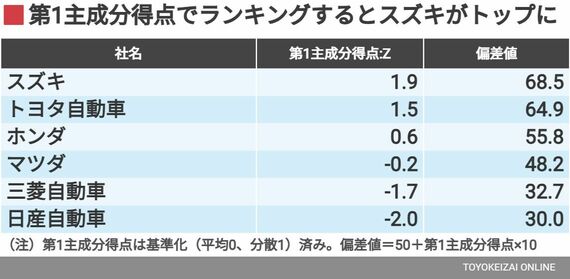
■この例で主成分分析を行うと4つの主成分（第1～第4主成分）が求められる

・ 第1主成分（Z^1）
Z1 ＝0.57×売上高営業利益率＋0.35×売上高増加率＋0.55×ROE＋0.51×自己資本比率
寄与率：65.3％

・ 第2主成分（Z^2）
Z2 ＝‐0.11×売上高営業利益率‐0.87×売上高増加率+0.39×ROE＋0.29×自己資本比率
寄与率：22.1％

・ 第3主成分（Z^3）
Z3 ＝‐0.53×売上高営業利益率＋0.20×売上高増加率‐0.29×ROE＋0.77×自己資本比率
寄与率：10.5％

・ 第4主成分（Z^4）
Z4 ＝0.62×売上高営業利益率‐0.30×売上高増加率‐0.68×ROE＋0.25×自己資本比率
寄与率：2.2％

（注）寄与率は、その主成分が全体の情報をどのくらい集約しているかを示す。第1主成分の寄与率は65.3％だったので、1つの主成分で全体の7割近くの情報を集約していることになる

他のランキング記事を見る