数学が苦手な人が陥る｢平均計算｣の落とし穴 暗記だけで済ます算数では理解は進まない

もう1つの相乗平均の考え方では、景気拡大の例が挙げられる。例えば、2002年2月に始まった景気拡大は2006年11月で58カ月目となり、1965年11月から4年9カ月にわたって続いた「いざなぎ景気」を超えたと当時言われた。

そして、2006年11月頃の新聞やテレビ報道などでは、4年9カ月にわたって続いた「いざなぎ景気」の年平均成長率は14.3％というものもあれば、11.5％というものもあった。かけ算の概念を基にする「平均経済成長率」という言葉の意味から、11.5％が正しく14.3％は間違いである。

間違いの本質はどこにあるのか

年平均成長率とは、かけ算の概念である「相乗平均」により答えを導く必要がある。成長する対象がこの期間全体を通して毎年同じ成長率で成長したとして、その期間の最後には最初から見て同じ成長になるような成長率を指す。

この間違いの本質は、問題1のそれと同じであり、問題1を作成した背景にはそのマスコミ報道の間違いに留意していたからである。

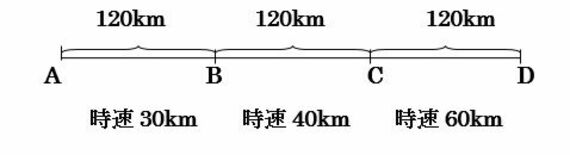
問題2の解説をしたい。平均とは「全体をならす」という意味である。この問題では、AB間は4時間、BC間は3時間、CD間は2時間で走行しているので、AD間（360km）の走行時間は9時間になる。そこでAD間における車の平均速度は、360÷9＝40と計算して、時速40kmである。

ある解答式は間違っているが、計算間違えをしたゆえに正解が出てしまったのである。マークシート試験ならば満点になるが、記述試験ならば0点である。長い大学教員人生で、途中式で2度間違ったから正解になった入試の記述式答案を何回か見たことが懐かしく思い出される。