｢灘中高｣は異次元の数学授業で秀才を育てる 折り紙でギリシャ3大作図不可能問題を解く

課題が進むと、ただ折り紙を折るだけではなく、代数的な計算も必要になる。3人組のうち1人が計算をして、1人が折り紙を折り、もう1人が実働部隊の2人に助言を与えるような分業体制をとっているグループが多い。

教室は、ワイワイ、ガヤガヤにぎやかだ。しかしうるさいわけではない。知的好奇心が刺激され、さらに友達同士で相乗効果をもたらし、にぎやかに数学の世界に没頭しているのがわかる。大講義室の空気が知的な振動を帯びている。

グループで協力しながら進んでいく

証明問題の解説はたったの30秒

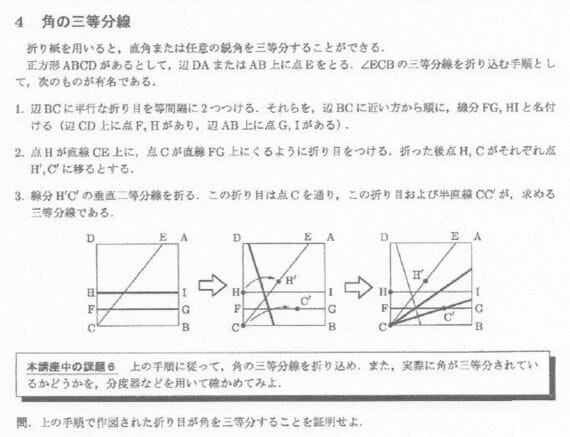
講座の目玉でもある「角の三等分問題」は課題6に登場する。コンパスと定規ではどうやってもできないことが、折り紙だとできる。それを体験する。

テキストの一部を抜粋転載する。実際に正方形の紙を使って、挑戦してみてほしい。作業自体は説明のとおりにやればできる。大切なのは「なぜそれで角の3等分ができているといえるのか」である。

作業自体ができたとしても、その理屈を証明できなければならない

「10時になりましたので、ざっと解説したいと思います。いったん折り紙を折るのをやめて、話を聞いてください。まず4ページで、角の三等分ができるという話です」

課題5までは一気に飛ばして、いきなり本題だ。

「いろんな証明が考えられますが、あっさりいきますね」

黒板にテキストと同じ図を描く。生徒たちも真剣な表情で黒板をにらむ。

「平行に折っているので、この角（∠FC’C）とこの角（∠C’CB）は錯角で等しいです。それから、ここ（線分CFと線分FH）は等しい長さで折っていますので、ここを結ぶ（線分HC’）とこの角（∠HC’F）とこの角（∠FC’C）が等しいです。あとはこういう対称軸（2番目の手順でできた折り目）がありますので、この角（∠HC’C）とこの角（∠H’CC’）が等しいです。終わり」