学校では習わない｢微分積分｣の意外すぎる活用法 実は電子体温計や桜の開花予想で使われていた

実は、微分法に比べて積分法の歴史は古く、古代ギリシャ時代にさかのぼります。

三角形や四角形など直線で囲まれた領域の面積を求めるのは、あまり難しいことではありませんよね。しかし、曲線で囲まれた領域の面積を求めるのは、簡単なことではありません。そこで、古代ギリシャの数学者で物理学者のアルキメデス（紀元前287頃～紀元前212頃）が、「取りつくし法」と呼ばれる方法を編み出しました。

取りつくし法とは、放物線の内側を無数の小さな三角形で埋め尽くし、その三角形の面積の総和を求めることで、間接的に放物線の内側の面積を求めるという方法です。この、「無限に小さい部分に分けて、それを足す」という考え方が、積分法の出発点となりました。

そして、その後、約1800年もの歳月を経て、アルキメデスの考え方を天文学に応用したのが、ドイツの天文学者ヨハネス・ケプラー（1571～1630）でした。

さらに、17世紀、ガリレオ・ガリレイの弟子のボナヴェントゥーラ・カヴァリエリ（1598～1647）が、「面」を無限に細かく分割していくと「線」になり、「立体」を無限に細かくしていくと「面」になることに気づき、「カヴァリエリの原理」を提唱しました。この考え方をもとに、その後、さまざまな数学者が積分法という形で発展させていったのです。

桜の開花予想は積分法でわかる

さて、微分法同様に、今や積分法もあらゆる分野において不可欠なものとなっています。たとえば、身近なものとしては、春になると出される「桜の開花予想」が挙げられます。桜の開花予想は、積分法を使って導き出すことができます。

桜の開花が気温と密接に関係していることは、日本では誰もが知っていることだと思いますが、「400℃の法則」や「600℃の法則」と呼ばれるものをご存じでしょうか。

400℃の法則とは、「2月1日からの日々の平均気温を足して、400℃に達した頃に桜が開花する」というもの、また、600℃の法則とは、「2月1日からの日々の最高気温を足して、600℃になる頃に桜が開花する」というものです。

ここで、たとえば600℃の法則に基づき、桜の開花日を予測します。

まず、2月1日から、その日の最高気温を記録していきます。そして、縦軸に最高気温、横軸に日にちをとり、グラフにしていきます。このとき、グラフの値を足し合わせていき、その累計が600℃に達した頃に、桜が開花すると予想されるというわけです。

『文系でも思わずハマる 数学沼』より

『文系でも思わずハマる 数学沼』（マガジンハウス）。書影をクリックするとアマゾンのサイトにジャンプします

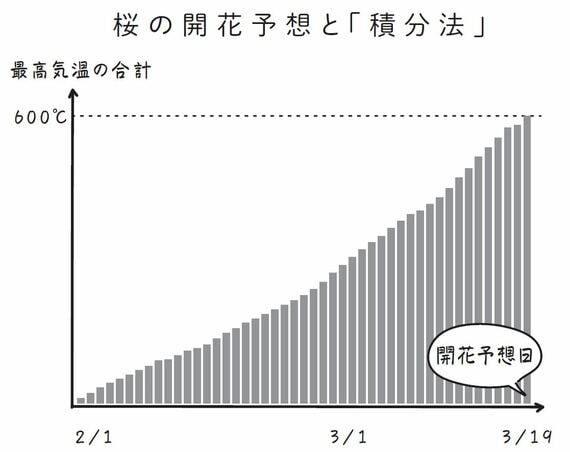
実際のところ、桜の開花には気温以外にもさまざまな要因が含まれるため、ここまで単純ではなく、現在、民間気象会社が各社で独自に計算式を作り、独自の開花予想を発表しているようです。しかし、基本的には積分が使われているということです。

なお、桜同様に、セミなどの昆虫も、ある一定の温度（これを「発育限界温度」といいます）以上になった日数を積算しているそうです。これを「有効積算温量」といい、この値がある値を超えると孵化や羽化を始めるそうです。桜も昆虫も積分をしていたのですね！