東大生が爆速で｢4桁の素因数分解｣解くカラクリ 才能ではなく｢テクニック｣と｢トレーニング｣

この式を使って考えてみると、「900－1」はこう変形できます。

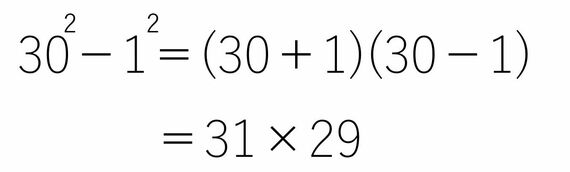
「900－1」＝「31×29」にできるわけですね。これより、「2697＝3×31×29」となるわけです。

ということで、2697の素因数分解ができるようになるためには、「2700－3と気づく」「そこから変形して、『900－1』が『30の2乗－1の2乗』の形だと気づく」「『30の2乗－1の2乗』の形からの変形で、31×29となることを見抜く」ということが必要だとわかります。

「工夫」は、トレーニングで「暗記」に変わる

その上で、何度か計算を繰り返していると、数自体を覚えてしまうようになります。

たとえば「899」＝「31×29」というのは、もう覚えてしまっているという人も多いです。何度も計算をしているうちに覚えてしまって、だからこそすぐに素因数分解ができるわけです。

さて、ここからご理解いただきたいのは、東大生が計算を速くできるのは、別に魔法を使っているわけでも、生まれつき天才だからでもないということです。

ちゃんとロジックがある上で、何度も経験しているからできるようになっている、ということなのです。