100年前の｢東大医学部入試｣は驚く程簡単だった ｢本当にこれが解答でいいのか？｣と心配になる

現代でいうと数学Ⅱで学習する「2倍角の公式」さえ知っていれば、答えることができます。

答えは、

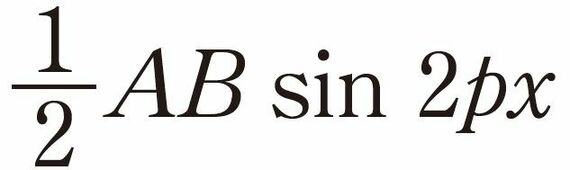
です。東大の医学部入試の問題にしては、「ほんとうにこれが解答でいいのか？」と心配になってしまうレベルの問題ですね。

さまざまな自然現象で見られる関数も出題

続いては、いろいろな方法が考えられる、複素数の冪乗（べきじょう）と複素数平面がテーマの問題です。

（出典：『100年前の東大入試数学 ディープすぎる難問・奇問100』）

旧字体で書かれているだけでなく問題文が非常に短いため、現代で出題されたら面喰らってしまうような問題です。でも、先の2問よりは難易度が上がるものの、実際にはそれほど難しい問題ではありません。

実数の3乗根で実数のものは1つだけしか存在しませんが、0でない複素数の3乗根で複素数のものは複数存在します。解く際には、このことに注意が必要です。

また、100年前当時は、微分に関連した問題も多く出題されました。東大の医学部入試もその例にもれず、そのなかのひとつが次の問題です。自然現象と深く結びついた関数のグラフがテーマです。

（出典：『100年前の東大入試数学 ディープすぎる難問・奇問100』）

現代の東大入試や医学部入試からは想像できないような平易さで、グラフを描くこと自体はいたって簡単です。

問題文にある関数形は、「粘性抵抗を受ける物体の落下運動」「1次反応の濃度変化」といった、さまざまな自然現象で姿を見せますので、このような関数形が登場する現象を考えながら解くとより楽しめます。当時の大学の先生方も、こうした数理モデルを思い描きながら問題を作成されたのかもしれません。

当時の入試数学のトレンドであり、東大入試数学においては全体のおよそ40％を占めていた積分関連の問題のなかにも、比較的解きやすい医学部入試数学の問題がありました。

（出典：『100年前の東大入試数学 ディープすぎる難問・奇問100』）

変数分離法という手法で解けるシンプルな微分方程式がテーマで、拙著の解説でも、シンプルな1階の常微分方程式を解くときの定番手法である変数分離法を紹介しています。

解答に際しては、分母が0になる可能性や解の一意性を詳しく検証するのはおいておき、定番の手法で微分方程式の解がひとつ求まればそれでヨシということにしています。

ここまで、東大医学部入試の問題でありながら、現代よりも難易度の低い問題を紹介してきました。

しかしながら、やはりレベルの高い問題も出題されていましたので紹介します。ひとつは、2定点からの距離の積が一定である曲線がテーマの問題です。

（出典：『100年前の東大入試数学 ディープすぎる難問・奇問100』）

旧字体や旧仮名遣いの問題文で、これも100年前当時ならではといえますが、x、y の方程式（や極方程式）ではなく、長さの積に関する条件式が与えられています。