東大入試で出題｢じゃんけんグリコ｣必勝法の衝撃 ｢小学校の算数｣で解ける問題を東大が出す意味

同様に、グーを出すときを考えると、勝ったときは3点、負けたときはパーで負けることになるので－6点となります。この3つの手をまとめると、このようになります。

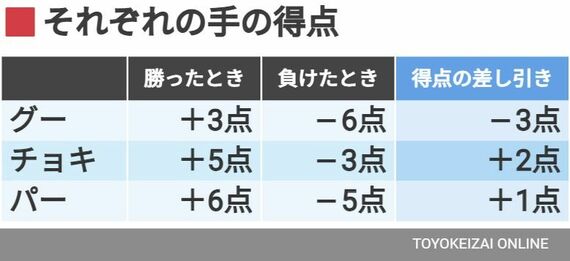
相手の手が完全にランダムである以上、勝ち負けも完全にランダムです。ということは、グーを出し続ければ点差は「－3点×ジャンケンの回数」に近づいていきますし、チョキを出し続ければ点差は「＋2点×ジャンケンの回数」に近づいていきます。

こう考えると、相手がランダムに手を出し続ける以上、チョキを出し続けるのがいちばん合理的な選択になるわけです。自分のことだけを考えるのであればたしかにパーが強そうに見えますが、実際はチョキのほうがいいわけですね。

表側だけでなく、「裏側」も見る思考法

さて、この問題は、「勝ったときだけでなく、負けたときにどうなるか」まで考えなければならない問題です。表側に見えているもの・自分の側だけでなく、裏側にあるものや相手の側に立って考える思考があるかどうかを問われていたと言えます。

じゃんけんグリコに限らず、どんなゲームでも、強くなるためには「相手の立場に立って考える思考」が必要だと言われています。将棋は相手がどう指すのかを先読みしながら指す必要がありますし、麻雀では相手の手牌がどんなものなのかを考えつつ自分の手牌を考えなければなりません。

こうした相手の立場に立って物事を考える思考は、「論理的思考力（ロジカルシンキング）」の1つとしてとらえられています。論理的に物事を考える中で、逆算的に思考する必要があるわけです。