クネクネの髪の毛を「定規一本」で計るやり方 東大教授伝授、小学生でもわかる微分・積分
この状態で子どもたちに定規だけを渡して、「この定規で髪の毛の長さを測ってください」と言います。すると、「できなーい!」「定規はまっすぐだからムリでーす!」と大騒ぎになります。
ですが、そこで答えを言わずに、「本当に? よく考えてごらん」としばらく考えさせると、ひらめく子が出てくる。「細かく分けて測ってみよう!」と。定規がまっすぐなのは変えられないので、まっすぐな定規で測れる範囲で、細かく見ていこうと思いつくんですね。
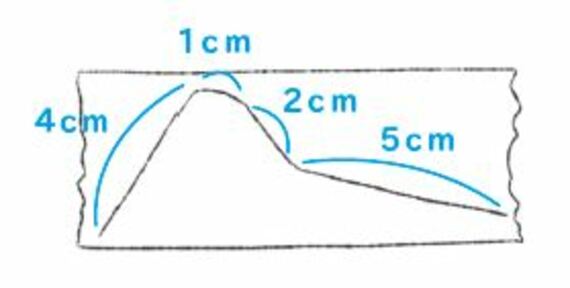
髪の毛の端からスタートして、最初の4㎝は直線っぽいな、次は少しカーブがきつくなるので1㎝くらいあててズラす、次は2㎝、次は5㎝かな、というようにやっていって最後に足せば、髪の毛の大体の長さはわかりますよね?
その発想を子どもたちが持てたら、私の授業の目的は達成したと言っても過言ではありません。
髪の毛は「長さ」のみですが、実際には昔の人が疑問に思った「この池ってどれくらい広いのかな~」といった「クネクネした形の面積を知りたい」というニーズから微積分がはじまったのではないかと思っています。面積に関しても考え方は同じで、「自分でも測れる、扱えるレベルまで分解する」という考え方が重要なポイントです。
このように、複雑なものでも細かく分ければ単純になる。単純になったら計測しやすいし、ムダも見つけやすい。それが終わったらまた足せばいい。それが微積分の本質的な考え方です。
この、小学生に配った定規というのは実は一次関数そのもので、いちばんシンプルな道具なわけです。中学で習う放物線で、さらにU字に曲がった線を測れるようになる。これが三次、四次となっていくとさらにグネグネした曲線を一発で測れるようになるわけですが、微分さえしてしまえば一次でコトが足りてしまうんです。
具体的に計算できるようになるにはもう少し授業が必要ですが、「使えるな~」「最強っぽいな~」ということが伝わればひとまず十分。特に大人が学び直すなら、「学んだらどうなるか?」「自分の生活に関係するのか?」という効果・効能みたいなものを先に知りたいですよね。
難解な公式は実はこんな意味だった
では、ここで実際に習った微分・積分の式を見てみましょう。微分は「d」を用いたこんな式を書きます。
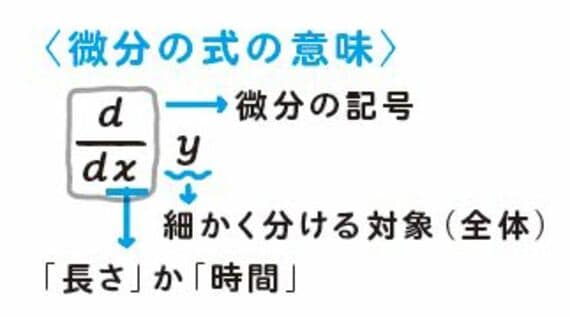
微分は「dx/d」が記号で、yが微分をする対象。yには髪の毛とか池といった「全体」が入ります。

































無料会員登録はこちら
ログインはこちら