クネクネの髪の毛を｢定規一本｣で計るやり方 東大教授伝授､小学生でもわかる微分･積分
ここで出てくるxは単位で見ずに「dx/d」がセットで、xの意味はたいてい「長さ」か「時間」。この表記全体を見たら「全体yを、長さか時間で細かく分けた結果」だと思ってください。
先ほどの例で言うと、「髪の毛1本を長さで細かく分けた結果」ということになります。
＜積分の式の意味＞
次に積分の式を見てみましょう。積分は英語の「S」を縦長にしたような独特の記号（インテグラル）を使います。
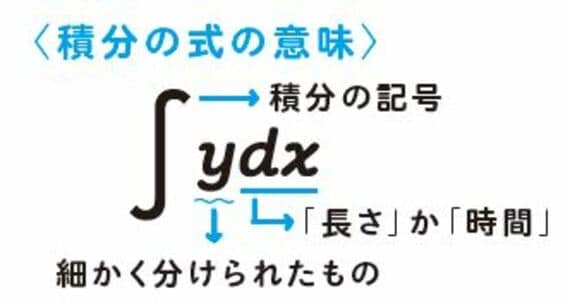
今度は積分なので、積分の対象となるyには「分けられたもの」が入ります。そして微分と同様に、dxというのはたいてい「長さ」か「時間」です。
つまりこの式は、「長さか時間で分けられたyを数えた結果」という意味になります。
微分は細かく分けるからyは「分ける対象（全体）」を表して、積分は集めて足していくからyには「分けられたもの」が入るということ。どうでしょう、なんとなくでも意味がつかめたのではないでしょうか？
二次関数ってそんなに単純なの？
ここで微積分の威力をわかってもらえる、もう少し具体的な話をしましょう。あまり深入りはしないので、大丈夫です。
まず、一次関数のグラフを描きます。一次関数は直線ですから、この直線とx軸の間にできる三角形の面積を求めたいと思ったら、「縦×横×1/2」をすればおしまいですよね。横が5、縦が4なら、「5×4×1/2＝10」。小学生でも解けます。
では、二次関数を描いた放物線はどうでしょうか？ 次のようなグラフがあって、曲線の下にできる面積を知りたいときはどのように求めればいいか、考えてみてください。
縦の値も横の値もわかる。でも、三角形みたいに単純に2で割ってしまうのは、凹んでいる分だけ小さくなるので、ちょっと違います。2で割れないとなるとどうすればいいか？答えは……なんと3で割ればいいんです。
え、そんな単純な？！と思いましたか？さらに衝撃的なことに、なんと、三次関数のときは4で割ればいい……！これがアルキメデスという知の巨人が教えてくれた人類への知恵なんです。
このように、過去の人々が長い時間をかけて解き明かしてくれたツールを使って、私たちは新たな課題解決に挑戦することができる。そう考えると、ロマンを感じませんか？
いかがでしょうか。数学嫌いのみなさんのハードルも少なからず下がったのではないでしょうか。こういった根本的な概念から具体的に学べば、数学は決して難しいものではありません。ぜひ、大人のみなさんも、今から数学の学び直しをしてみてください。きっと楽しいですよ。
