全国学力テストから見えた｢子どもの学力｣2大弱点､説明力と批判的思考力 国語､算数･数学､理科に共通する大きな課題

記述式設問の正答率から見えてくる「説明力」の弱さ

今回の調査で日本の子どもたちの学力の弱点がいっそう明確になってきた。それは国語と算数・数学、さらには理科にも共通する弱点だ。

1つ目の弱点は、「説明力」である。説明というとただの表現の問題だと思われがちだが、それだけではなく思考力の弱さとも深く関わる。そして、何を問われているのか、求められているのかを理解する「読解力」の弱さでもある。記述式の設問の中でも、とくに正答率が低かった設問を中心に具体的に少し見ていこう。

正答率が低かった設問の1つが、小学校算数の2の（4）の設問である。ここでは果汁の変化に伴う飲み物の量の変化を問うている。まず、次の「ゆうかさん」の気づきが示される。

小学校算数 2の（4）

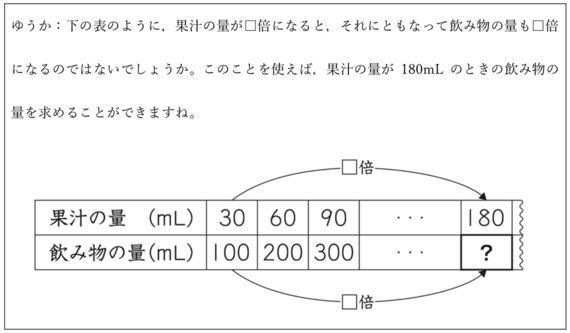
そのうえで、以下の設問が示される。

「何mlか」の正答は「600ml」で、その求め方の正答例は「果汁の量は、180÷30＝6で、6倍になっています。果汁の量が6倍になると飲み物の量も6倍になるので、飲み物の量は、100×6＝600で、600mlになります」だ。それほど難易度は高くないはずだが、正答率は48.0％である。「600ml」と答えを出すことはできても、「どのように求めたのかがわかるように」「求め方を式や言葉」を使って説明することができていない。

説明には、3つの要素が必要となる。まず「果汁の量は、180÷30＝6で、6倍になっています」という倍率についての説明。その上で「果汁の量が6倍になると飲み物の量も6倍になる」という果汁と飲み物の量が比例の関係にあることの説明が続く。最後に「飲み物の量は、100×6＝600で、600mlになります」という計算式と結論が必要となる。

600mlと答えられていても、1つめの倍率の説明が欠落していたり、2つ目の比例の説明が欠落していたりするケースが多い。合わせて20.0%近くの子どもがこれらの理由で正答にならなかった。

これらは、算数・数学の授業で計算の意味を言葉で説明させる指導が、十分に行われていないことが原因と考えられる。それでも以前に比べ、算数・数学で言葉による説明を取り入れる授業が増えてきている。しかし、説明をさせても、その説明にはどういう要素が必要なのか、逆にその説明のどこに不十分さがあるかを子どもたちに意識させる授業はまだ少ない。それゆえ子どもたちは部分的に説明できたとしても、十分な説明には到達できない。