｢掛け算の順序問題｣はやっぱり決着がつかない 5×4が正解のとき4×5がバツになる不思議

この「1あたり」と「いくつ分」は、文部科学省「【算数編】小学校学習指導要領（平成29年告示）解説」（以下、学習指導要領解説）や教科書でも出てくる表現である（「1あたり」は「1つ分の数」「1つ分の大きさ」などと表記されることが多い）。学習指導要領の解説では「1皿に5個ずつ入ったみかんの4皿分の個数」が例に出されているが、この答えを求める場合、「1つ分の数」は「5個」であり「いくつ分」は「4皿」だ。「1つ分の数」×「いくつ分」で式を構成すると、以下になる。

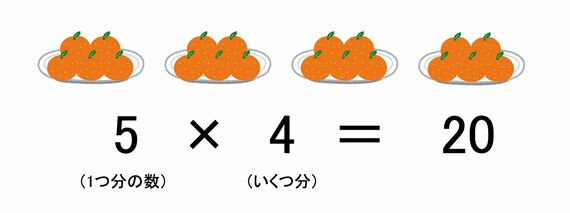
前出の遠山啓氏の主張にのっとれば、この式が「4×5」でも問題ないはずだ。ところが、「1つ分の数」×「いくつ分」の式の順序で考えると、本来「いくつ分」であるべき「4」を「1つ分の数」と捉えてしまいかねない。そうなると、下記のようになる。

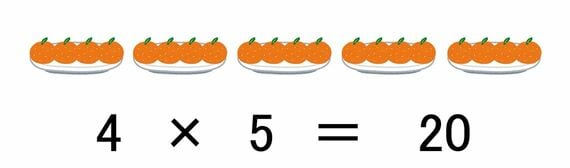
5×4でも4×5でも答えは同じ20だが、式の順序を変えると「1皿に5個ずつ、4皿」なのが「1皿に4個ずつ、5皿」となってしまうおそれがあるというわけだ。

なお、学習指導要領解説では「ここで述べた被乗数と乗数（※3）の順序は、『一つ分の大きさの幾つ分かに当たる大きさを求める」という日常生活などの問題の場面を式で表現する場合に大切にすべきことである』と記されている。解釈の仕方によっては、順序を間違えないように指導してほしいと読み取れなくもないが、文科省初等中等教育局教育課程課に取材したところ、返答はこうだった。

※3 被乗数と乗数は「かけられる数とかける数」、つまり「一つ分の数といくつ分」のこと。

「順序がどうというよりも、掛け算がどういうもので、それぞれの数が何を意味しているのかを理解することが大切です。そのうえで、学校現場でどう指導するかは各学校のやり方にもよるでしょうし、児童の状況や理解度を踏まえながらご指導いただく必要があると思っています」（文科省初等中等教育局教育課程課）

バツにせず、注釈を書き込む教員も

では、学校現場ではどう教えているのだろうか。

「私が小学2年生の担任をしていた時は、式の順序が違っていてもバツにしませんでしたし、点数も下げませんでした。バツをつけて保護者からクレームが来るのも嫌だなという意識はありましたね」

そう答えるのは、首都圏の小学校で教鞭を執るA氏。1965年および72年に起きた論争をはじめ、近年も毎年のようにSNSへ答案をアップしているのがたいてい保護者であることを踏まえれば、クレームを恐れるのも当然だろう。ただ、もう少し深く話を聞くと、掛け算の意味を伝えたいという意識を強く持っていることがわかる。

「交換法則もあるので、たとえ順序が違ってもバツにするほどのことではないと思っています。ただし、『1つ分の数』と『いくつ分』で意味が違うのは確かなので、そこは子どもたちに理解してほしいですね。だから、式の順序が違う答えにバツをすることはありませんでしたが、矢印を書き込んで『順番が違うよ』と伝えるようにしていました」