物事の本質は｢2次関数｣学ぶと理解が早くなる訳 私立文系はとくに知ってほしい｢数学｣の重要性

マーケティングや営業の分野では、広告費などの費用をいくらかければ売り上げや利益を最大化できるかといったことがよく問われます。サンプルデータを基にそうした課題を解くための分析手法として回帰分析があり、その基礎となっている最小2乗法では、やはり2次関数が使われます。

『教養としての「数学I・A」』（NHK出版）。書影をクリックするとAmazonのサイトにジャンプします。

文系分野であっても、数字に裏づけられた業務を担当するのであれば、基礎となる2次関数をしっかり学んでおいて損はありません。

また、2次関数は物理現象と密接な関係があります。

一定の速度で走る自動車が1時間走ったときの距離は、「速さ×時間」で求まります。これは中学校で習った等速直線運動です。

ところが、物体が自由落下するとき、あるいは物体が坂道を転がり落ちるときは、加速度がついて速度が増していくため、等加速度直線運動になります。この等加速度直線運動での移動距離はどうなるでしょうか。

1つの考え方として、ごく短い等速運動を積み重ねるというやり方があります。下の図を見てください。等速運動する時間をどんどん短くしていくと、等加速度直線運動の移動距離は、速度と時間のグラフに現れる台形の面積を求めればよいということがわかります。

出所：『教養としての「数学Ⅰ・A」』

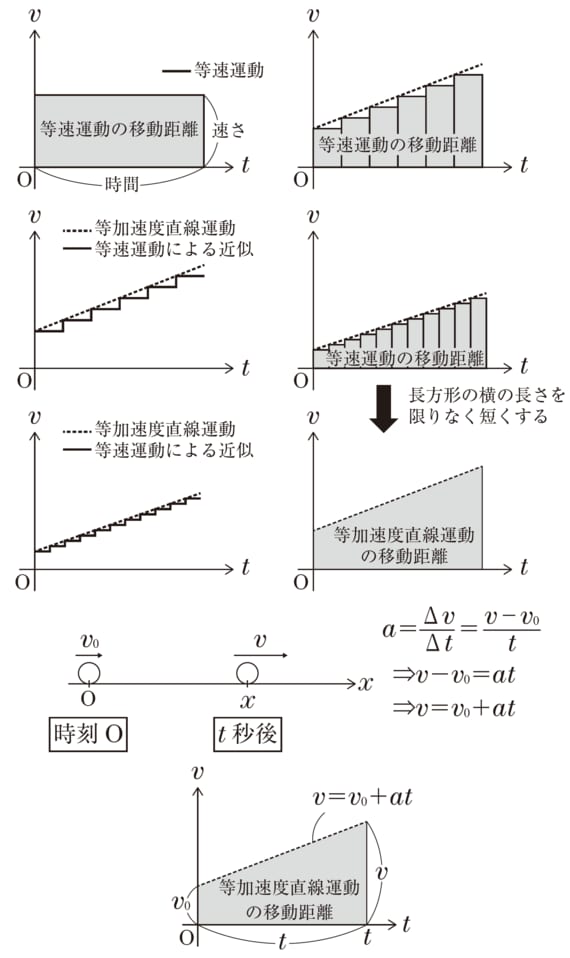
この世のほとんどは「非線形」

また、物体を投げたときの曲線は――放物線といわれているように――必ず2次関数で表されます。さまざまな物理現象を解き明かすために、2次関数は不可欠です。

ほかにも数学Ⅱ・Bの範囲にはなりますが、統計においても2次関数が出てきます。身長と体重の関係などさまざまなデータの相関を調べていると、正規分布と呼ばれる曲線が登場してきます。その標準正規分布の式は次のようになります。

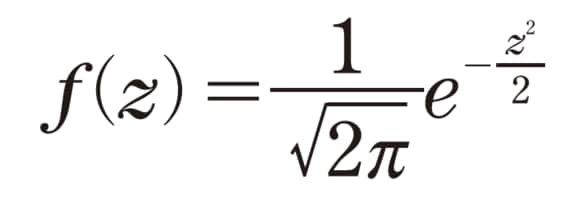
この中にも2次関数が隠れているのです。

社会現象、物理現象のほとんどは、「線形」ではなく「非線形」です。線形というのは、y=ax+bといった1次式、つまり直線のグラフで表される関係です。一方の非線形は線形でない、もっと複雑な関数を指します。2次関数は、私たちが非線形に触れる第一歩といえるでしょう。

このように、2次関数はビジネスのみならず、この世の現象を解き明かすために密接に関わっているのです。