物事の本質は｢2次関数｣学ぶと理解が早くなる訳 私立文系はとくに知ってほしい｢数学｣の重要性

数学が実社会でいかに役立ち、論理的思考力の形成にどのように貢献するのか――。例えば、関数を例にとってみましょう。関数の理解は因果関係を緻密に考えられる力につながります。yがxの関数であるとき、xとyの関係は原因と結果の関係と捉えることができるからです。

そもそも関数とはいったい何でしょうか。この「かんすう」、昔は「函数」と書いていました。函数という用語は元々中国語で、英語のfunctionを音訳した当て字だといわれています。年配の数学者の中には、関数よりも函数を好んで使う人が少なくありません。「函」には箱という意味があり、これが関数の本質をよくとらえているからです。

教科書では、「2つの変数x、yがあって、xの値を定めるとそれに対応してyの値がただ1つ定まるとき、yはxの関数であるという」となっています。

「函数」のイメージをつかむには、自動販売機を思い浮かべていただくのがいいでしょう。

自動販売機のボタンを押すと、あるボタンに対応する商品が出てきます。同じボタンを押しているのに押すたびに違う商品が出てきたら、安心して買い物できません。どのボタンを押しても、必ずそのボタンに対応する商品が出てくる。それが信頼できる自動販売機の条件です。

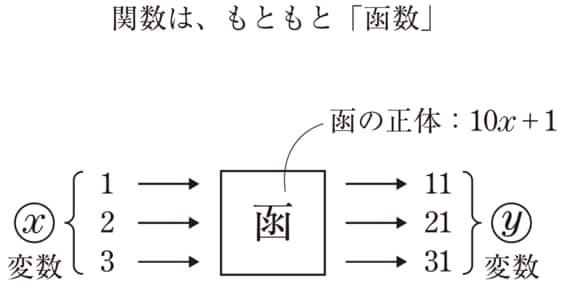
関数というのは、こういう信頼できる自動販売機のような「箱」だと思ってください。この箱、関数にいろんな値を入れていくとしましょう。例えば、1を入れたときは11、2を入れたときには21、3を入れたときに31が出てくるとします。この箱に入れる値をまとめてx、出てくる値をyとすれば、この箱の正体はy=10x+1だとわかります

出所：『教養としての「数学Ⅰ・A」』

さまざまなシチュエーションで顔を出す2次関数

さらに数学Ⅰで習うような2次関数を平方完成させて、グラフを描き、さらに最大値や最小値を求める――、そんな状況はまずないだろうと思うかもしれません。ところが、文系、理系を問わず、2次関数はさまざまなシチュエーションで顔を出します。

共通テストが実施される前に行われた平成29年度試行調査（プレテスト）で、なかなか面白い2次関数の問題が出されていました。実際に出題されたのは長めの文章題でしたが、内容を要約すると、文化祭で売るTシャツ1枚の価格をいくらにすれば最も売れるかを考えるというものです。

事前アンケートで、価格設定に応じて購入したいという人の数も変化することがわかりました。Tシャツ1枚の価格をx円、売れる枚数をy枚としたとき、yとxは次のような関係になったというのです（もちろん、これはあくまでも仮定の話です）。

出所：『教養としての「数学Ⅰ・A」』

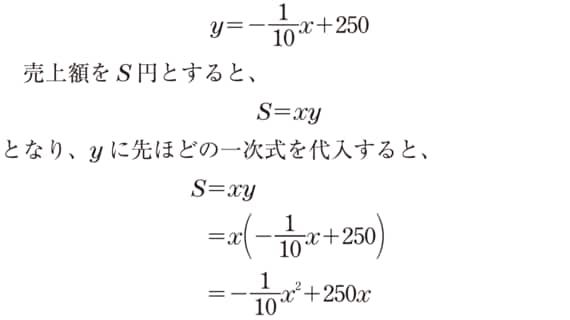
つまり、この問題は売り上げを2次関数で表現し、それを最大化するTシャツの価格、x円を求めるという狙いでした。売り上げを最大化しようとする際に2次関数の問題が出てくるというのは、文系出身の社会人にとっても興味深い例ではないでしょうか。